Blog Bitix
rss x github
Cabecera

Los autómatas del juego de la vida de Conway y la hormiga Langton con su implementación en Java

Escrito por el .
java planeta-codigo programacion
Enlace permanente Comentarios

Algunos procesos que aparentemente son complejos siguen reglas muy simples, y aún siguiendo reglas muy simples dan lugar a muchos posibles comportamientos diferentes. Los sistemas que implementan y aplican estas reglas simples se les conoce como autómatas. Los autómatas no poseen inteligencia artificial, no aprenden ni toman decisiones en base a anteriores resultados, los autómatas simplemente siguen sus reglas de comportamiento en el estado del sistema. Dos autómatas conocidos son el juego de la vida de John Horton Conway publicado en 1970 y la hormiga de Langton de Chris Langton publicado en 1986.

Contenido del artículo

El juego de la vida de Conway

El juego de la vida de Conway es un autómata con unas reglas muy simples que da lugar a múltiples y variados comportamientos. Es un autómata de cero jugadores que se desarrolla por sí mismo en base al estado inicial y las reglas del juego.

El juego es un tablero bidimensional formado por cuadrados o células que poseen dos estados, células muertas o encendidas o células vivas o apagadas. Cada célula está rodeada por 8 células vecinas. El estado de las células evoluciona a lo largo de unidades de tiempo discretas, el estado de todas las células se tiene en cuenta para calcular el estado en el turno siguiente aplicando las reglas del juego. Todas las células se actualizan simultáneamente en cada turno.

Reglas

Las reglas del juego de la vida definido por Conway son las siguientes:

  • Una célula muerta con exactamente 3 células vecinas vivas nace, en el siguiente turno estará viva o encendida.
  • Una célula viva con 2 o 3 células vecinas vivas sigue viva.
  • En cualquier otro caso la célula muere o se apaga, por tener menos o más células adyacentes vivas de las reglas anteriores. Una célula viva muere por soledad o por superpoblación.

Variaciones, con otras reglas

El juego de la vida definido por Conway se representa con la siguiente nomenclatura 23/3, los primeros dos números indican las células necesarias para que una célula siga viva y el tercer número indica las células adyacentes necesarias para que una célula nazca.

Con otro número de células requeridas es posible crear variaciones del juego de la vida. Por ejemplo, 16/6 en el que una célula nace si tiene 6 vivas adyacentes y sigue viva si tiene un número igual a 1 o 6. Otra variación es 23/36 en el que una célula nace si el número de adyacentes vivas es 3 o 6 y sigue viva si el número de células vivas es 2 o 3, este caso es similar al juego de la vida de Conway variando que una célula nace si tiene 6 adyacentes vivas.

Patrones

Dado el estado inicial y las reglas de juego de la vida se observan varios patrones de comportamiento.

  • Osciladores: estos patrones siguen una serie de pasos hasta que un número determinado llega al estado inicial, el patrón se repite de forma cíclica.
  • Vidas estáticas: estas no cambian de estado con el paso del tiempo se mantienen en el mismo estado con el paso del tiempo.
  • Naves espaciales: estos patrones evolucionan dando la sensación de que se trasladan por el tablero de juego de la vida.
  • Matusalenes: son patrones que evolucionan o desaparecen después de un gran número grande de turnos.
  • Cañones: son patrones que generan planeadores o naves espaciales.
  • Locomotoras: son patrones que se desplazan por el tablero dejando un rastro de basura de osciladores, vidas estáticas, planeadores o naves espaciales.
  • Sintetizadores: son patrones que dispuestos de elementos más básicos como gliders producen otro tipos de patrones.

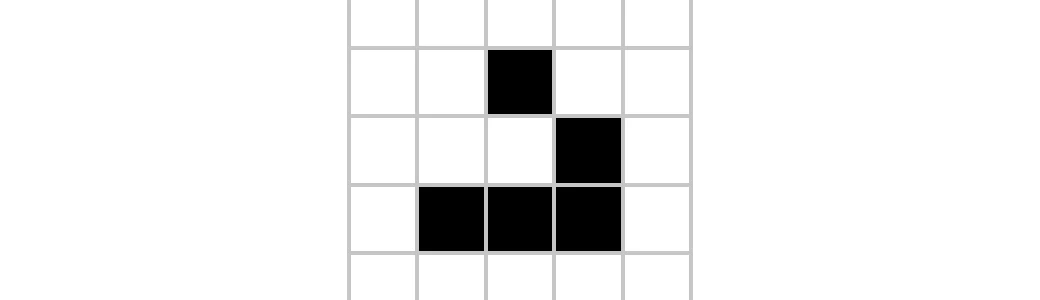
Uno de los patrones destacados del juego de la vida es una nave espacial conocido como glider, este es un patrón importante ya que son fáciles de producir que se pueden hacer colisionar con otros objetos de este modo ser usados para transmitir información. Ocho gliders pueden ser posicionados para que colisionen formando un cañón gosper glider. Otros patrones como bloques, beehives, blinkers, traffic lights son sintetizables con únicamente dos gliders.

Los gliders también son capaces de colisionar para producir otros comportamientos, si dos gliders son lanzados contra un bloque de la forma adecuada el bloque se mueve hacia a la fuente de los gliders. Si tres glider son disparados en la forma correcta el bloque se mueve más aún. Esta memoria de desplazamiento puede ser usada para simular un contador modificable lanzándole gliders. También es posible construir puertas lógicas como AND, OR o NOT usando gliders. Esto es la misma capacidad de computación que una máquina universal de Turing, de modo que usando gliders el juego de la vida es de forma teórica tan capaz como cualquier computadora con memoria ilimitada y sin restricciones de tiempo. Por estas propiedades del glider se ha adoptado como un icono de la cultura hacker.

En esta librería de patrones del juego de la vida de Conway hay una colección de patrones en la que además es posible visualizar su comportamiento.

Glider Glider gun Diehard

Patrones glider, glider gun y diehard

Patrones que crecen indefinidamente Patrones que crecen indefinidamente Patrones que crecen indefinidamente

Patrones que crecen indefinidamente

Otros patrones:

Cómo probar el juego de la vida

En algunas páginas es posible probar el juego de la vida para experimentar con su comportamiento.

La hormiga de Langton

La hormiga de Langton es otro tipo de autómata con unas reglas muy simples pero que da lugar a un comportamiento complejo. Al igual que el juego de la vida de Conway se desarrolla en un tablero de dos dimensiones en el que cada celda del tablero está encendida o apagada.

En está página de la wikipedia se puede probar la hormiga de Langton.

Hormiga de Langton

Patrón generado por la hormiga de Langton después de 10K pasos

Reglas

La hormiga de Langton se basa en las siguientes reglas:

  • Si está sobre un cuadrado encendido, cambia el color del cuadrado, gira noventa grados a la izquierda y avanza un cuadrado.
  • Si está sobre un cuadrado apagado, cambia el color del cuadrado, gira noventa grados a la derecha y avanza un cuadrado.

En el caso de la hormiga de Langton al cabo de unos 10000 turnos crea un patrón que sigue de forma indefinida.

Variaciones, con otras reglas

A la hormiga de Langton también es posible aplicarle otra reglas, por ejemplo añadiendo más estados a las celdas con colores o incluyendo varias hormigas en el tablero.

Implementación del juego de la vida en Java

Esta es la implementación en código con lenguaje Java del juego de la vida de Conway y sus reglas. Estas son las clases principales que implementan el juego, la clase Cell representa una célula con su estado y la clase Board en el método step produce el siguiente estado con las reglas del juego implementadas en los métodos survives, borns y countAliveNeighbours.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

package io.github.picodotdev.blogbitix.javaconwaylangton.conway;

public class Cell {

    public enum Status {
        ALIVE, DEAD
    }

    private Status status;
    private int age;

    public Cell() {
        this(Status.DEAD);
    }

    public Cell(Status status) {
        this(status, 0);
    }

    public Cell(Status status, int age) {
        this.status = status;
        this.age = age;
    }

    public boolean isAlive() {
        return status == Status.ALIVE;
    }

    public void setAlive() {
        this.status = Status.ALIVE;
        this.age = 0;
    }

    public boolean isDead() {
        return status == Status.DEAD;
    }

    public void setDead() {
        this.status = Status.DEAD;
        this.age = 0;
    }

    public int getAge() {
        return age;
    }

    public void tick() {
        age += 1;
    }

    public Status getStatus() {
        return status;
    }
        
    public void setStatus(Status status) {
        if (this.status != status) {
            age = 0;
        }
        this.status = status;
    }
}
conway/Cell.java 
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123

package io.github.picodotdev.blogbitix.javaconwaylangton.conway;

...

public class Board {

    private Collection<Integer> aliveRules = List.of(2, 3);
    private Collection<Integer> bornRules = List.of(3);
    private Cell[][] cells;

    public Board(String initial) {
        this(initial, 160, 80);
    }

    public Board(String initial, int width, int height) {
        initCells(width, height);
        loadCells(initial);
    }

    public Cell getCell(int x, int y) {
        if (y < 0 || y > getHeight()) {
            return null;
        }
        if (x < 0 || x > getWidth()) {
            return null;
        }
        return cells[y][x];
    }

    public int getWidth() {
        return cells[0].length;
    }

    public int getHeight() {
        return cells.length;
    }

    public int getPopulation() {
        int population = 0;
        for (int y = 0; y < getHeight(); ++y) {
            for (int x = 0; x < getWidth(); ++x) {
                if (getCell(x, y).isAlive()) {
                    population += 1;
                }
            }
        }
        return population;
    }

    public void step() {
        Cell[][] cells = new Cell[getHeight()][getWidth()];
        for (int y = 0; y < getHeight(); ++y) {
            for (int x = 0; x < getWidth(); ++x) {
                Cell oldCell = getCell(x, y);
                Cell newCell = new Cell(oldCell.getStatus(), oldCell.getAge());
                cells[y][x] = newCell;
                int aliveNeighbours = countAliveNeighbours(x, y);
                Cell.Status status = (survives(oldCell, aliveNeighbours) || borns(oldCell, aliveNeighbours)) ? Cell.Status.ALIVE : Cell.Status.DEAD;
                newCell.setStatus(status);
            }
        }
        this.cells = cells;
    }

    private boolean survives(Cell cell, int aliveNeighbours) {
        return cell.isAlive() && aliveRules.contains(aliveNeighbours);
    }

    private boolean borns(Cell cell, int aliveNeighbours) {
        return cell.isDead() && bornRules.contains(aliveNeighbours);
    }

    private int countAliveNeighbours(int x, int y) {
        return (int) getNeighbours(x, y).stream().filter(Cell::isAlive).count();
    }

    private Collection<Cell> getNeighbours(int x, int y) {
        Collection<Position> positions = new ArrayList<>();
        for (int j = y - 1; j < y + 2; ++j) {
            for (int i = x - 1; i < x + 2; ++i) {
                if (i == x && j == y) {
                    continue;
                }
                if (i < 0 || i > getWidth() - 1 || j < 0 || j > getHeight() - 1) {
                    continue;
                }
                positions.add(new Position(i, j));
            }
        }
        return positions.stream().map(p -> getCell(p.getX(), p.getY())).filter(Objects::nonNull).collect(Collectors.toList());
    }

    private void initCells(int width, int height) {
        this.cells = new Cell[height][width];
        for (int y = 0; y < height; ++y) {
            for (int x = 0; x < width; ++x) {
                this.cells[y][x] = new Cell(Cell.Status.DEAD);
            }
        }
    }

    private void loadCells(String initial) {
        int width = Arrays.stream(initial.split("\\n")).max(Comparator.comparing(s -> s.length())).orElseGet(() -> "").length();
        int height = initial.split("\\n").length;

        int x = (getWidth() / 2) - (width / 2);
        int y = (getHeight() / 2) - (height / 2);

        for (int i = 0, a = 0, b = 0; i < initial.length(); ++i) {
            Character c = initial.charAt(i);
            if (c == '\n') {
                a = 0;
                b += 1;
            } else if (c != ' ') {
                Cell cell = getCell(x + a, y + b);
                cell.setStatus(Cell.Status.ALIVE);
                a += 1;
            } else {
                a += 1;
            }
        }
    }
}
conway/Board.java

Implementación de la hormiga de Hormiga de Langton en Java

Esta es la implementación en lenguaje Java de la hormiga de Langton y las reglas propias del juego. La clase Turmite representa la hormiga, el método step aplica la lógica del autómata de la hormiga en función del estádo de la celda en la que está. Los metodos turnLeft, turnRight y forward cambian el estado de la hormiga haciéndola cambiar de dirección y avanzando a otra celda.

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105

package io.github.picodotdev.blogbitix.javaconwaylangton.langton;

public class Turmite {

    public enum Direction {
        UP, DOWN, LEFT, RIGHT
    }

    private int x;
    private int y;
    private Direction direction;

    public Turmite() {
        this(80, 24, Direction.UP);
    }

    public Turmite(int x, int y, Direction direction) {
        this.x = x;
        this.y = y;
        this.direction = direction;
    }

    public int getX() {
        return x;
    }

    public int getY() {
        return y;
    }

    public Position getPosition() {
        return new Position(x, y);
    }

    public boolean isAt(int x, int y) {
        return this.x == x && this.y == y;
    }

    public void step(Board board) {
        Cell cell = board.getCell(x, y);
        if (cell == null) {
            return;
        }
        if (cell.isOn()) {
            cell.setOff();
            turnLeft();
            forward();
        } else if (cell.isOff()) {
            cell.setOn();
            turnRight();
            forward();
        }
    }

    public void forward() {
        switch (direction) {
            case UP:
                this.y -= 1;
                break;
            case DOWN:
                this.y += 1;
                break;
            case LEFT:
                this.x -= 1;
                break;
            case RIGHT:
                this.x += 1;
                break;
        }
    }

    public void turnLeft() {
        switch (direction) {
            case UP:
                this.direction = Direction.LEFT;
                break;
            case DOWN:
                this.direction = Direction.RIGHT;
                break;
            case LEFT:
                this.direction = Direction.DOWN;
                break;
            case RIGHT:
                this.direction = Direction.UP;
                break;
        }
    }

    public void turnRight() {
        switch (direction) {
            case UP:
                this.direction = Direction.RIGHT;
                break;
            case DOWN:
                this.direction = Direction.LEFT;
                break;
            case LEFT:
                this.direction = Direction.UP;
                break;
            case RIGHT:
                this.direction = Direction.DOWN;
                break;
        }
    }
}
langton/Turmite.java
Terminal

El código fuente completo del ejemplo puedes descargarlo del repositorio de ejemplos de Blog Bitix alojado en GitHub.

Referencia:

Comparte el artículo:

Artículos relacionados:

El patrón de diseño Factory, ventajas sobre new y diferencias con Builder

El patrón de diseño Factory, ventajas sobre new y diferencias con Builder
Repositorio de artefactos privado con Nexus

Repositorio de artefactos privado con Nexus
Autenticación con OpenID/OAuth en cualquier web con Nginx y de forma nativa con Spring Boot

Autenticación con OpenID/OAuth en cualquier web con Nginx y de forma nativa con Spring Boot
Crear un archivo Zip con Java, comprimir y descomprimir datos

Crear un archivo Zip con Java, comprimir y descomprimir datos
Emitir trazas de las peticiones y respuestas HTTP con clientes Java

Emitir trazas de las peticiones y respuestas HTTP con clientes Java
Cómo deduplicar eventos de dominio

Cómo deduplicar eventos de dominio